けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 168 C - : (Colon) (4Q, 灰色, 300 点)

AtCoder AtCoder300点 ABC-C 三角関数 式変形 中学受験典型 計算幾何 灰色diff 円 三角形 数学(図形問題) 浮動小数点型を扱う問題 NoviSteps4Q

余弦定理を使うか、座標を求めるか、、、いずれにしても三角関数の素養を要求する問題。

問題へのリンク

問題概要

時計の時針と分針があって、それぞれ長さは A, B となっている。 H 時 B 分の段階において、時針の先端と分針の先端との距離がどのようになっているかを求めよ。

制約

  • 1 \le A, B \le 1000

解法 1： 余弦定理

まず一つの観察として、

三角形の二辺の長さと、それを挟む角度がわかっていたら、三角形の形が決まるはずだ

つまり、下図の赤線の長さがわかるはずだ！！！

というのがある。

これを実際に求める方法を与えるのが、数学 1 で学ぶ「余弦定理」である。

【余弦定理】
上図の赤線の長さは、

\sqrt(A^{2} + B^{2} - 2AB \cos{\theta})

となる

余弦定理は「三平方の定理」を一般化したものになっている。具体的には、 \theta を直角とすると、 \cos{\theta} = 0 なので、赤線の長さは \sqrt(A^{2} + B^{2}) になる。これは三平方の定理そのもの！！

いずれにせよ、余弦定理を見ると、 \theta さえ求められればよいということがわかる。

角度 θ

時針の角度 \alpha と、分針の角度 \beta をそれぞれ求めてあげて、その差を求めればよい。一見すると、

  • \alpha と \beta の大小関係で場合分け
  • \theta が 180 度を超えるかどうかで場合分け

が必要なように思えてしまうかもしれない。

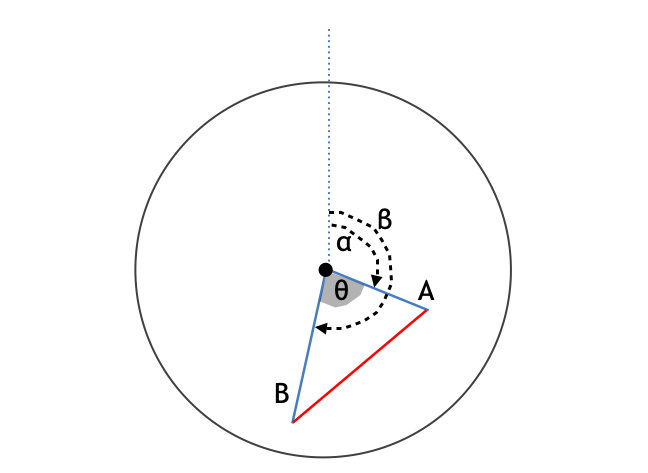
しかしながら、

  • \cos(- \theta) = \cos \theta　(ゆえに、 \alpha と \beta の大小関係は気にしなくてよい)
  • \cos(2 \pi - \theta) = \cos \theta　(ゆえに、 \theta が 180 度を超える側になっても問題ない)

といったことが成り立つ。よって、

  • \theta = \alpha - \beta

として、 \sqrt(A^{2} + B^{2} - 2AB \cos{\theta}) を計算すればよい。

時針の角度 α の求め方

時針は 12 時間 (= 720 分) で 360 度回転する。よって、そのうちの 60H + M 分時点での角度 \alpha は、

\alpha = \frac{60H + M}{720} × (2\pi)

と求められる。ここで、以下のように間違えないように注意！！

(間違い) \alpha = \frac{H}{12} × (2\pi)

これだと、1 時間おきに時針が、「一気に動いて」「止まって」を繰り返す不自然な動きになってしまう。

分針の角度 β の求め方

分針は 60 分で 360 度回転する。よって、そのうちの M 分時点での角度 \beta は、

\beta = \frac{M}{60} × (2\pi)

で求められる。

まとめ

以上をまとめると、以下のようにして O(1) で解ける

  • \alpha = \frac{60H + M}{720} × (2\pi) として、
  • \beta = \frac{M}{60} × (2\pi) として、
  • \theta = \alpha - \beta として、
  • 答えは \sqrt(A^{2} + B^{2} - 2AB \cos{\theta})

なお、円周率 \pi は、acos(-1.0) の値を用いるのが簡明。

#include <bits/stdc++.h>
using namespace std;

const double PI = acos(-1.0);
int main() {
    double A, B, H, M;
    cin >> A >> B >> H >> M;
    double alpha = (H * 60 + M) / 720 * (PI * 2);
    double beta = M / 60 * (PI * 2);
    double theta = alpha - beta;
    double res = sqrt(A*A + B*B - 2.0*A*B*cos(theta));
    cout << fixed << setprecision(10) << res << endl;
}

解法 2： 2 点の座標を求めて距離を算出する

計算幾何に慣れている人にとっては、こっちの方がむしろ自然な解法だと思う。計算幾何は基本的に「点」と「線分」を扱う。その観点からは

  • なんらかの定義づけがなされた「点」の座標を一つ一つ求めていく

というのが自然なアプローチだと思う。その観点から言うと、今回の問題も

  • 時針の先端の座標 (x_{A}, y_{A})
  • 分針の先端の座標 (x_{B}, y_{B})

を求めてあげれば、その二点間の距離を

\sqrt((x_{A}-x_{B})(x_{A}-x_{B}) + (y_{A}-y_{B})(y_{A}-y_{B} ) )

によって求めることができる (二点間の距離の公式を参照)。

単位円と座標

最後に、時針・分針の先端の座標を求める方法を考えよう。その前に単位円を用いた三角関数の定義を確認しておく。

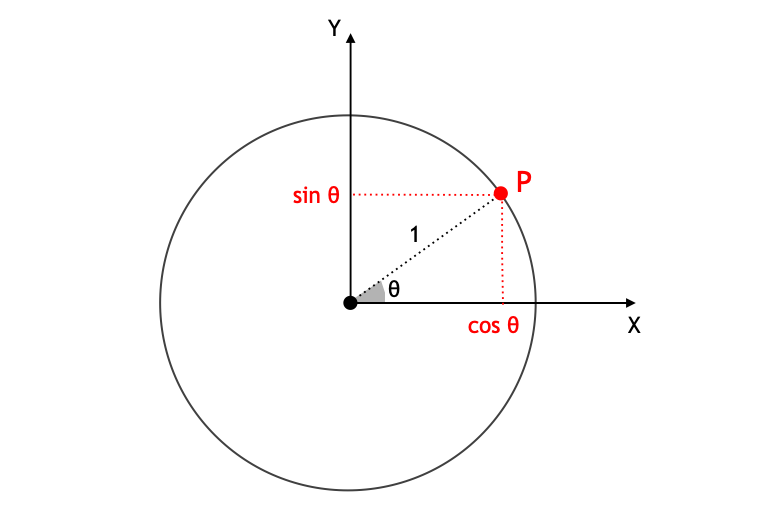
上図のように、円の半径を 1 として、X 軸とのなす角が \theta であるような円周上の点を P とする。このとき、P の座標を

(\cos \theta, \sin \theta)

とする。むしろこっちの方が、高校数学の範囲では汎用的な三角関数の定義といえる (この記事参照)。そして円の半径が A のときは、P の座標は

(A \cos \theta, A \sin \theta)

となる。

今回の問題だと

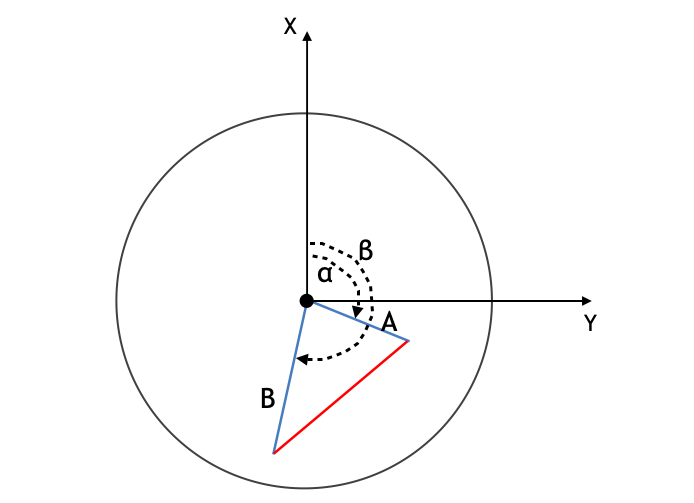
今回の問題では、下図のように X 軸、Y 軸をとれば OK。そうすると、単純に、

  • 時針の先端の座標は、 (A \cos \alpha, A \sin \alpha)
  • 分針の先端の座標は、 (B \cos \beta, B \sin \beta)

と求められる。0 時の方向に X 軸を合わせるイメージ。そして針の進行方向に Y 軸を持ってくるイメージ。

まとめ

以上をまとめると、以下のようにして O(1) で解ける

  • \alpha = \frac{60H + M}{720} × (2\pi) として、
  • \beta = \frac{M}{60} × (2\pi) として、
  • 時針の先端の座標は、 (x_{A}, y_{A}) = (A \cos \alpha, A \sin \alpha)
  • 分針の先端の座標は、 (x_{B}, y_{B}) = (B \cos \beta, B \sin \beta)
  • 答えは \sqrt((x_{A}-x_{B})(x_{A}-x_{B}) + (y_{A}-y_{B})(y_{A}-y_{B} ) ) となる
#include <bits/stdc++.h>
using namespace std;

const double PI = acos(-1.0);
int main() {
    double A, B, H, M;
    cin >> A >> B >> H >> M;
    double alpha = (H * 60 + M) / 720 * (PI * 2);
    double beta = M / 60 * (PI * 2);
    double xA = A * cos(alpha), yA = A * sin(alpha);
    double xB = B * cos(beta), yB = B * sin(beta);
    double res = sqrt((xA-xB)*(xA-xB) + (yA-yB)*(yA-yB));
    cout << fixed << setprecision(10) << res << endl;
}