「積の和」典型の、最も典型的な問題

将来、「積の和」タグを開いたときに、最も典型的な問題が目に入るように。なお、二項係数 を と表記することにする。

問題概要

長さが で総和が であるような、正の整数のみからなる数列 は 通り考えられる。これらすべての数列についての

の総和を 998244353 で割ったあまりを求めよ。

制約

• 

解法 (1)：積の和典型

求めたい値は、次のように組合せ論的解釈ができる。一般に、積を数え上げ問題における「積の法則」に対応させることで、積の和を組合せ論的に解釈できることがよくある。

---

個の一列に並んだマスを、

• 個の区間に分割し、
• 各区間からマスを 1 個ずつ選んで赤く塗る

という方法が何通りあるか？

---

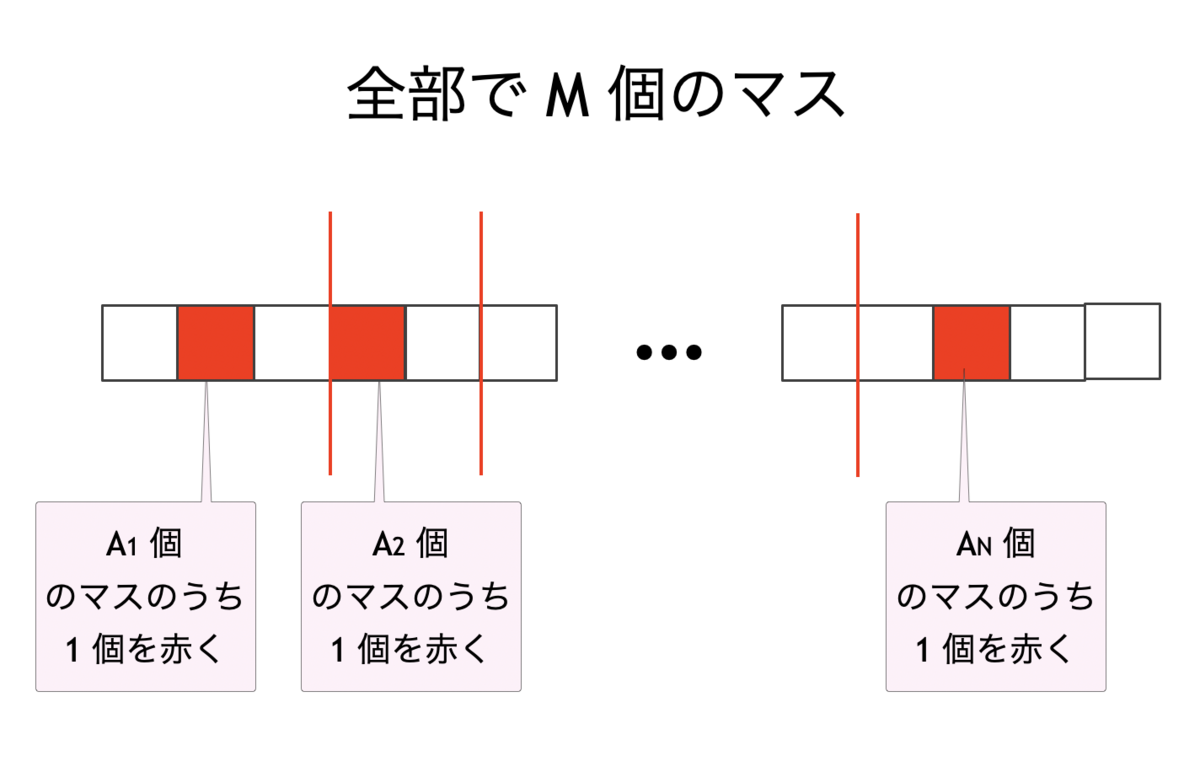
これはさらに言えば、下図のように、区間を分割するために切れ目 ( 個ある) を「赤いマス」と同一視してしまうことによって、次の値に一致することが分かる。

---

個のマス (赤色マスが 個、白色マスが 個) がある。これらを並び替えて得られる模様は何通りあるか？

---

この答えは 通り と求められる。

解法 (2)：FPS

FPS を用いて求めることもできる。求めたい値は、FPS を用いて次のように表せる。

ここで、 とおく。 を掛けたものを引くことで、

となる。よって、

と求められる。ゆえに、求めたい値は

と表せる。この値は、負の二項係数を用いて、

---

---

と書ける。一般に となるから、求める値は結局次のようになる。解法 (1) で得た値に一致する。

---

---

コード

#include <bits/stdc++.h>
using namespace std;

// modint
template<int MOD> struct Fp {
    // inner value
    long long val;
    
    // constructor
    constexpr Fp() noexcept : val(0) { }
    constexpr Fp(long long v) noexcept : val(v % MOD) {
        if (val < 0) val += MOD;
    }
    constexpr long long get() const noexcept { return val; }
    constexpr int get_mod() const noexcept { return MOD; }
    
    // arithmetic operators
    constexpr Fp operator - () const noexcept {
        return val ? MOD - val : 0;
    }
    constexpr Fp operator + (const Fp &r) const noexcept { return Fp(*this) += r; }
    constexpr Fp operator - (const Fp &r) const noexcept { return Fp(*this) -= r; }
    constexpr Fp operator * (const Fp &r) const noexcept { return Fp(*this) *= r; }
    constexpr Fp operator / (const Fp &r) const noexcept { return Fp(*this) /= r; }
    constexpr Fp& operator += (const Fp &r) noexcept {
        val += r.val;
        if (val >= MOD) val -= MOD;
        return *this;
    }
    constexpr Fp& operator -= (const Fp &r) noexcept {
        val -= r.val;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr Fp& operator *= (const Fp &r) noexcept {
        val = val * r.val % MOD;
        return *this;
    }
    constexpr Fp& operator /= (const Fp &r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b, swap(a, b);
            u -= t * v, swap(u, v);
        }
        val = val * u % MOD;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr Fp pow(long long n) const noexcept {
        Fp res(1), mul(*this);
        while (n > 0) {
            if (n & 1) res *= mul;
            mul *= mul;
            n >>= 1;
        }
        return res;
    }
    constexpr Fp inv() const noexcept {
        Fp res(1), div(*this);
        return res / div;
    }

    // other operators
    constexpr bool operator == (const Fp &r) const noexcept {
        return this->val == r.val;
    }
    constexpr bool operator != (const Fp &r) const noexcept {
        return this->val != r.val;
    }
    friend constexpr istream& operator >> (istream &is, Fp<MOD> &x) noexcept {
        is >> x.val;
        x.val %= MOD;
        if (x.val < 0) x.val += MOD;
        return is;
    }
    friend constexpr ostream& operator << (ostream &os, const Fp<MOD> &x) noexcept {
        return os << x.val;
    }
    friend constexpr Fp<MOD> modpow(const Fp<MOD> &r, long long n) noexcept {
        return r.pow(n);
    }
    friend constexpr Fp<MOD> modinv(const Fp<MOD> &r) noexcept {
        return r.inv();
    }
};

// Binomial coefficient
template<class T> struct BiCoef {
    vector<T> fact_, inv_, finv_;
    constexpr BiCoef() {}
    constexpr BiCoef(int n) noexcept : fact_(n, 1), inv_(n, 1), finv_(n, 1) {
        init(n);
    }
    constexpr void init(int n) noexcept {
        fact_.assign(n, 1), inv_.assign(n, 1), finv_.assign(n, 1);
        int MOD = fact_[0].get_mod();
        for(int i = 2; i < n; i++){
            fact_[i] = fact_[i-1] * i;
            inv_[i] = -inv_[MOD%i] * (MOD/i);
            finv_[i] = finv_[i-1] * inv_[i];
        }
    }
    constexpr T com(int n, int k) const noexcept {
        if (n < k || n < 0 || k < 0) return 0;
        return fact_[n] * finv_[k] * finv_[n-k];
    }
    constexpr T fact(int n) const noexcept {
        if (n < 0) return 0;
        return fact_[n];
    }
    constexpr T inv(int n) const noexcept {
        if (n < 0) return 0;
        return inv_[n];
    }
    constexpr T finv(int n) const noexcept {
        if (n < 0) return 0;
        return finv_[n];
    }
};

int main() {
    const int MOD = 998244353, MAX = 610000;
    using mint = Fp<MOD>;
    
    int N, M;
    cin >> N >> M;
    
    BiCoef<mint> bc(M+N);
    cout << bc.com(M+N-1, M-N) << endl;
}