0. はじめに

プログラミングコンテストにおいて、連立一次方程式を解くことに帰着できる問題は数多く出題されています。

連立一次方程式は Gauss Jordan の掃き出し法によって解くことができるのですが、「その解の個数を求めよ」などと言われたときに詰まりがちな印象があったので、簡単に解説してみます。

なお、掃き出し法を要求する問題は競プロでは「実数」「 ${\mathbb F}_2$ 」「mod. p」の 3 パターンがあるイメージです。特に「解の個数を求めよ」という問題に関しては、 $n$ を変数の個数として

係数	解の個数
実数	一般には無限個
${\mathbb F}_2$	$2^{n - {\rm rank}}$
mod. $p$	$p^{n - {\rm rank}}$

となります。ここで、 ${\mathbb F}_2$ は ${\rm mod}. p$ の特殊な場合 ( $p = 2$ ) なのですが、出題も多く bitset を用いた高速化なども決まったりするので特別扱いしています。

1. 掃き出し法が目指すもの

まずは、掃き出し法が何をするためのアルゴリズムなのかについて、概説します。

1-1. 標準形

掃き出し法とは連立一次方程式を解くときに基本となるアルゴリズムです。例えば

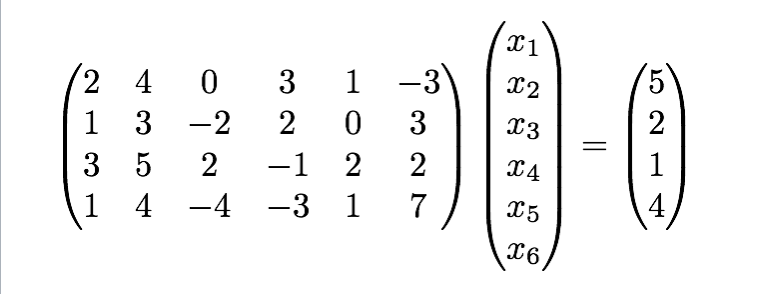
f:id:drken1215:20190318175951p:plain

のような連立一次方程式を変形して

f:id:drken1215:20190318180003p:plain

のような形にすることを目指しています。このような形を標準形と呼びます。標準形にしてしまえば、パラメータを用いて解を自然に表すことができます。上の例で言えば、 $x_3 = t_1, x_6 = t_2$ とすると、以下のように求められます。競プロ的に言えば「 $x_3$ と $x_6$ の値を決めてしまえば、残りの変数の値は一意に決まる」という状態です。

f:id:drken1215:20190319143101p:plain

この場合、2 つのパラメータで解を表現しているので、「自由度は 2 である」といいます。自由度が「解の個数」に直接関係して来る雰囲気が見て取れます。

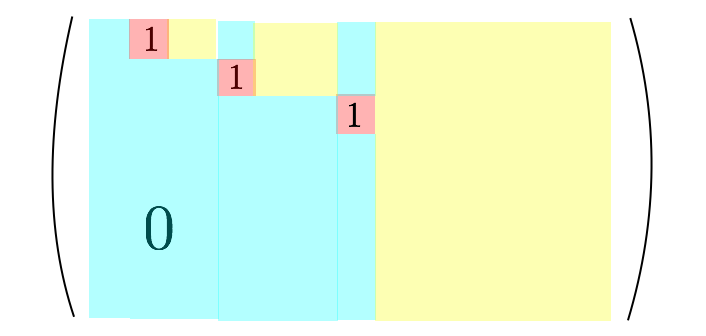
標準形は一般に以下のような形を目指します¹。下図で、水色の部分はすべて $0$ で、黄色の部分はどんな数値でもよいです。また、「 $1$ 」のところはピボットとも呼ばれ、ピボットの列についてはすべてを $0$ にします (ピボットの上の方にも 0 が伸びています)。

f:id:drken1215:20190319130031p:plain

ここで、行列のランクとは、上図で言えば「 $1$ の個数」に対応します。ランクには様々な等価な意味づけがありますが、ここでは

行列の線形独立な行ベクトルの最大本数

という意味づけがピッタリ対応していてわかりやすいでしょう。すなわち、 $1$ のある行の個数です。「行列の線形独立な行ベクトルの本数」は、掃き出し法を行っても不変なまま保たれるので、掃き出し法を行う前の行列のランクと、掃き出し法を行った後の行列のランクはもちろん一致します。

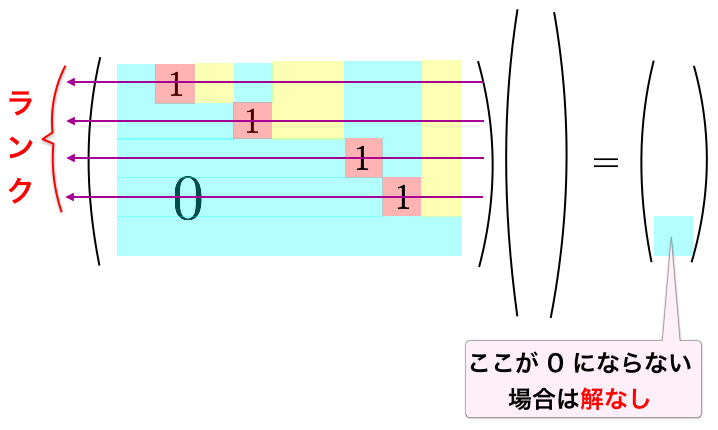
f:id:drken1215:20190319125919p:plain

注意点として、一般には掃き出し法を行ったときに、下段の方は「一行すべて $0$ 」であるような行が何行か並ぶことがあります。その場合は右辺のそれに対応する部分も $0$ になる必要があります。そうでない場合は「解なし」です。このような状況は例えば

$x + 2y = 5$
$2x + 4y = 3$

のような方程式で発生します。上の式を $2$ 倍したものを下ののから引くと、

$0 = -7$

になってしまい、矛盾です。よってこの方程式を満たす $x, y$ は存在しないということになります。

標準形から具体的な解をパラメータで表すには下図のように、赤く示した列に対応する変数をパラメータで置いてあげます。これは最初の例で言えば、 $x_3 = t_1, x_6 = t_2$ と置いたことに対応しています。

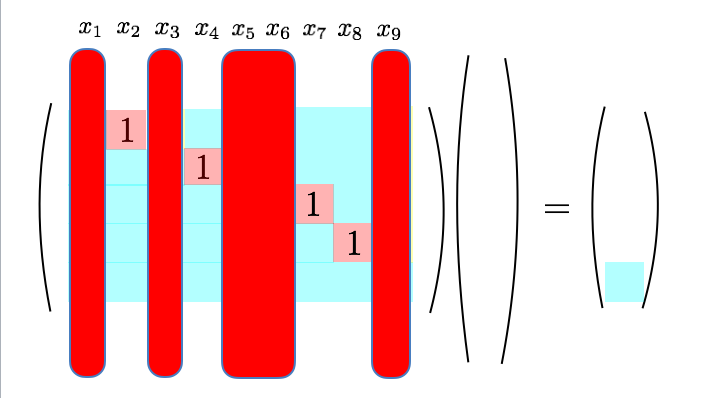
f:id:drken1215:20190319125040p:plain

さてここまで来ると、「 ${\mathbb F}_2$ 」「 ${\rm mod}. p$ 」での連立方程式の解の個数の意味が明快になります！すなわち

(列の本数) - (1 の個数) の分だけ、パラメータを設定する
よって、(行の本数) = (変数の個数)、(1 の個数) = ランクであることから、自由度は $n - {\rm rank}$ となる
${\mathbb F}_2$ では各パラメータの取りうる値は $2$ 通りあるので解の個数は $2^{n - {\rm rank}}$ であり、 ${\rm mod}. p$ では各パラメータの取りうる値は $p$ 通りあるので解の個数は $p^{n - {\rm rank}}$ となる

というストーリーです。

1-2. 数学的な補足を少し

標準形の一意性

標準形と言うからには「どのような順番で掃き出し操作を行っても、出来上がる標準形は一意に定まる」という一意性が成り立っていてほしいです。もちろん成り立ちます。

他にも様々な標準形

本記事で述べる標準形は、以下の行基本変形と呼ばれる操作に関する標準形です:

行を swap する
ある行を定数倍する
行 $p, q$ と定数 $a$ について、 $p$ を $p + aq$ で置き換える

他にも様々な「操作」を定めると、それに応じた様々な「標準形」が生まれます。以下に例をあげます。関心のある方は「伊理正夫: 線形代数汎論」の「6 章: 行列の標準形と応用」に詳しいです。

Jordan 標準形 (いわゆる対角化を対角化できない行列にも拡張したもの)
特異値標準形
Sylvester 標準形
Hermite 標準形、Smith 標準形
DM 分解

行列を線形写像だと思うと...

TL を眺めていると、しばしば ${\rm ker}(A)$ や ${\rm dim}$ ${\rm ker}(A)$ という表記を見かけると思います。これは行列を線形写像だと思ったときに登場する概念たちです。行列を線形写像だと思うことで、ランクの持つ意味がよりハッキリするというメリットがありますし、圧倒的に豊かな線形代数の世界が拡がっていきます。しかしながら、単に連立方程式を解くモチベーションにおいてはそこを理解していなくても大丈夫そうです。

2. 行基本変形

私たちは与えられた行列に対し、行基本変形と呼ばれる操作を好きな回数だけ好きな順序を繰り返すことで以下の標準形に変形させたいです。なお、連立方程式を解く文脈では右辺のベクトルもまとめて変形します。これは左辺の行列に右辺のベクトルを連結させた行列 (拡大係数行列と呼びます) に対して行基本変形を施していると思えば自然です。

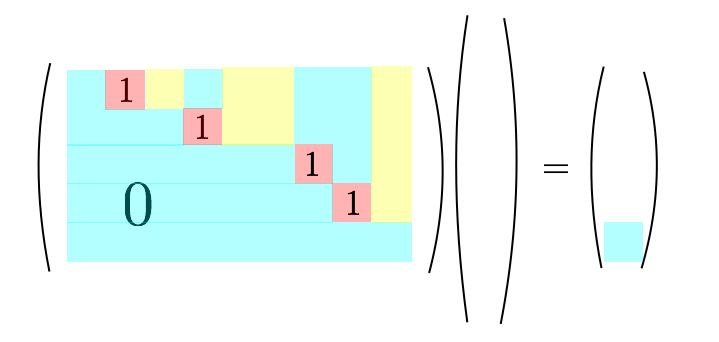
f:id:drken1215:20190319131356p:plain

原理的には行基本変形をどのような順序で繰り出しても、標準形は一意に決まるので、どんな順序だろうと標準形に持って行ければそれでよいです。しかしながら、システマティックに標準形に変形できるアルゴリズムを与えた方がよいでしょう。それが掃き出し法です。掃き出し法に立ち入る前にまずは行基本変形をおさらいしてみます。以下の 3 つの操作です。

2-1. 行の swap

行と行を swap する操作です

f:id:drken1215:20190319132452p:plain

これは連立方程式に立ち戻ると、完全にそれはそうで、

$2x_1 + 3x_2 + 4x_3 - x_4 = 1$
$7x_1 + x_2 - 5x_3 + 2x_4 = 9$
$3x_1 - 2x_2 + 4x_4 = -6$

という連立方程式の 2 個目と 3 個目の式を入れ替えただけですね。

$2x_1 + 3x_2 + 4x_3 - x_4 = 1$
$3x_1 - 2x_2 + 4x_4 = -6$
$7x_1 + x_2 - 5x_3 + 2x_4 = 9$

2-2. 行を定数倍

行を定数倍します。これもそれはそうな感じです。

f:id:drken1215:20190319133312p:plain

2-3. 行 p を定数倍して行 q に加える

いよいよ行基本変形の中核となる式変形です。ある行を定数倍したものを、他の行に足し上げる操作です。その使い道のイメージを例示します。

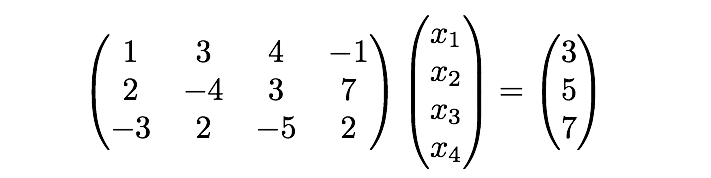
f:id:drken1215:20190319142836p:plain

上のような行列において、1 行目を $-2$ 倍したもの

$-2x_1 - 6x_2 - 8x_3 + 2x_4 = -6$

を 2 行目に足すと以下のようになります:

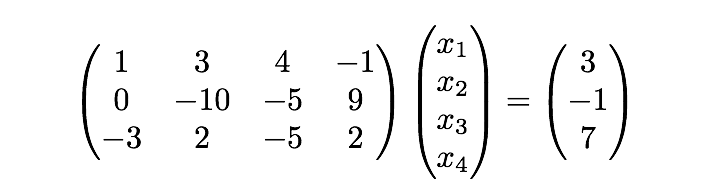
f:id:drken1215:20190319135003p:plain

同様に 1 行目を $3$ 倍したものを 3 行目に足すと以下のようになります:

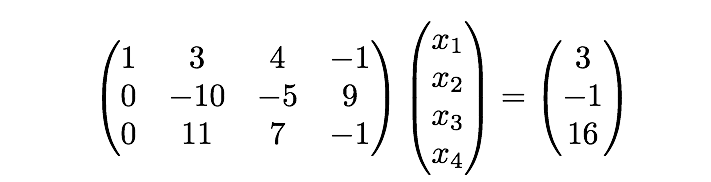
f:id:drken1215:20190319142858p:plain

こんな風にして、この場合左上の $1$ をピボットとして、その列をすべて $0$ にしてしまうことができます。これが掃き出し法の重要なステップになります。

3. Gauss-Jordan の掃き出し法

いよいよ具体的なアルゴリズムです。蟻本に載っているものを拡張して、

変数の個数と方程式の本数が一致しない場合
解が存在しない場合
解の個数も求める場合 (ランクや行列式も)

などにも対応できるようにして行きます。

さて、掃き出し法の途中過程は下図のようになっています。3 個目のピボットについて、その列をすべて掃き出して $0$ にした状態です。

f:id:drken1215:20190319170409p:plain

これから 4 個目のピボットになるやつを探し出す作業を行います。下図のように、太赤枠の範囲内で非零要素を探します。太赤枠の範囲内で左から順に列全体を見ていき、

その列内に非零要素が存在しないうちは、右に進めて行く

というようにします。そして非零要素が見つかったらそれを次のピボットに選びます。

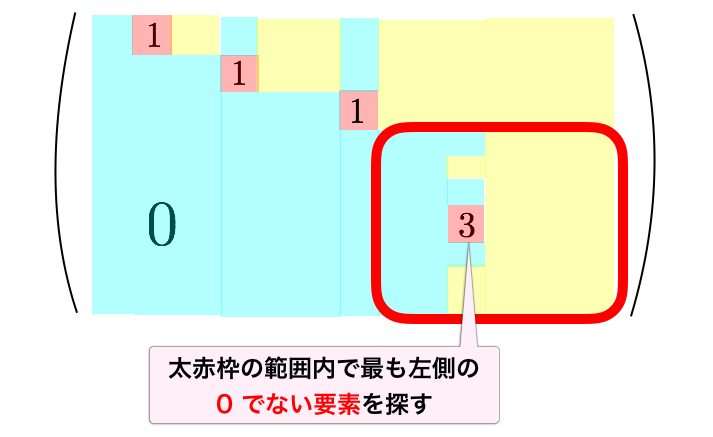
f:id:drken1215:20190319170459p:plain

注意点として、数値誤差の観点からは

あるピボットが見つかったとき、同じ列に他の非零要素があるかもしれない。どのピボットを選ぶべきか？

という問題が発生します。数学的にはどれを選んでも最終的に得られる結果は等しくなりますが、数値誤差を考える必要のある状況では重要な問題意識です。しかしながら今回は特に気にせず、どれを選んでも良いことにします。

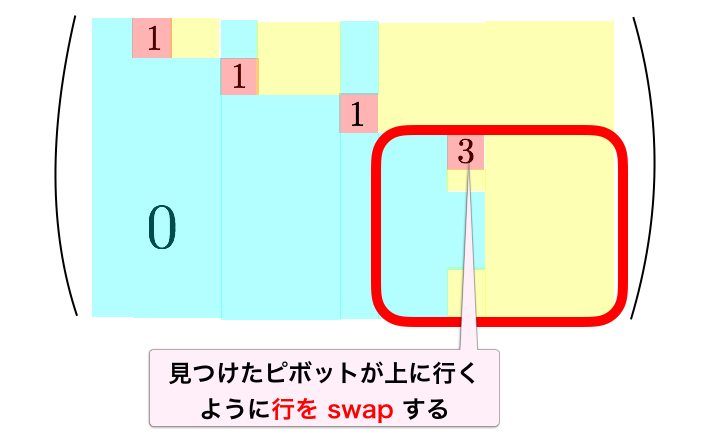
ピボットを見つけたら、まずはピボットが上に行くように行を swap します。具体的には、赤太枠の中で最も上の行と swap します。ここでは行基本変形の 1 個目の操作を使っています。

f:id:drken1215:20190319173434p:plain

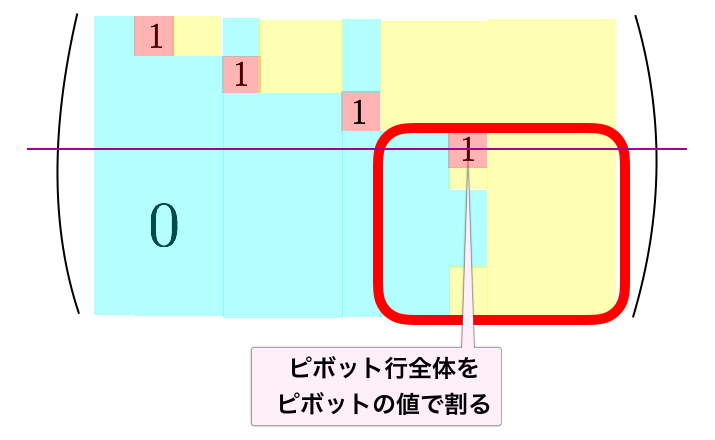
そしてその行全体をピボットの値で割ります。そうするとピボットの値が $1$ になります。これは行基本変形の 2 個目の操作を使っています。

f:id:drken1215:20190319173524p:plain

最後に、行基本変形 2-3 の節で示した方法によって、ピボットのある列の値がすべて $0$ になるように掃き出しを行います。

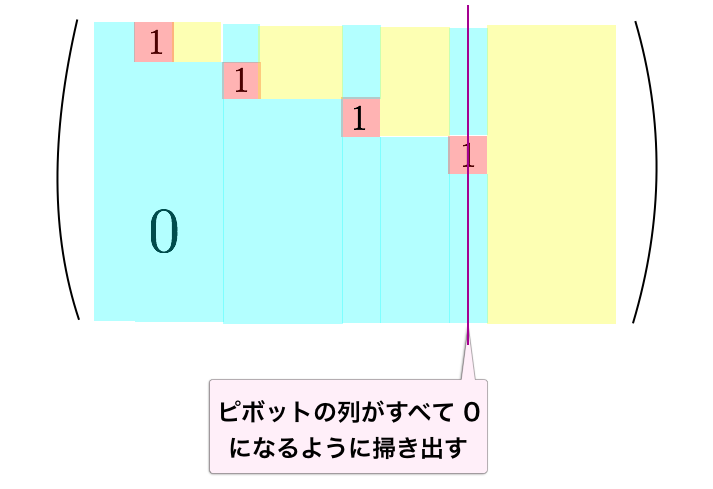
f:id:drken1215:20190319173545p:plain

ここまで来ると、また次のピボットを選ぶフェーズに戻っていることがわかります。以上の操作をピボットを選べなくなるまで繰り返します。

計算量は行数を $R$ 、列数を $C$ とすると $O(RC^{2})$ となります。

4. Gauss-Jordan の掃き出し法の実装

行列の各要素が「実数の場合」「 ${\rm mod}. p$ の場合」「 ${\mathbb F}_2$ の場合」のそれぞれの場合について見てみます。

なお、以下の実装はいずれも github で公開しています:

github.com

実数の場合： algorithm/matrix_double.cpp at master · drken1215/algorithm · GitHub
${\rm mod}. p$ の場合： algorithm/matrix_modp.cpp at master · drken1215/algorithm · GitHub
${\mathbb F}_2$ の場合： algorithm/matrix_binary.cpp at master · drken1215/algorithm · GitHub

4-1. 実数の場合

実数の場合の特有の事情として、「非零かどうかの判定」がとても厄介です。そんな事情もあってか今の所は、「ランクを求めよ」といった出題はほとんどなくて、

正則行列 $A$ が与えられて連立一次方程式 $Ax = b$ の解を求める (解は 1 個しかない)

という設定が多い気がします。代表例としては蟻本にも載っている「ランダムウォークで戻ってくるまでの回数の期待値」を計算する問題などがあります。

実数係数の場合について、行列 $A$ を標準形に変形する処理は以下のように実装できるでしょう。実数の場合特有の事情として、

ピボット選択時に非零要素を選ぶところで、ゼロかどうかの判定を実施するための定数 EPS を定義している
abs(v) < EPS であれば v = 0 であると判断している
ピボットが存在する列においてピボットを選ぶときは、数値誤差を緩和する観点から絶対値が最大のものを選ぶようにしている

といった点が挙げられます。また他の実装上の注意点として、掃き出す対象の行列が「拡大係数行列」であった場合には、ピボット選択が最後の列 ( $Ax = b$ の $b$ の部分) まで来たときは掃き出さずにそのままにしています。

#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <iomanip>
#include <algorithm>
using namespace std;
#define COUT(x) cout << #x << " = " << (x) << " (L" << __LINE__ << ")" << endl


using D = double;
const D EPS = 1e-10;

// matrix
template<class T> struct Matrix {
    vector<vector<T> > val;
    Matrix(int n, int m, T x = 0) : val(n, vector<T>(m, x)) {}
    void init(int n, int m, T x = 0) {val.assign(n, vector<T>(m, x));}
    size_t size() const {return val.size();}
    inline vector<T>& operator [] (int i) {return val[i];}
};

template<class T> int GaussJordan(Matrix<T> &A, bool is_extended = false) {
    int m = A.size(), n = A[0].size();
    int rank = 0;
    for (int col = 0; col < n; ++col) {
        // 拡大係数行列の場合は最後の列は掃き出ししない
        if (is_extended && col == n-1) break;

        // ピボットを探す
        int pivot = -1;
        T ma = EPS;
        for (int row = rank; row < m; ++row) {
            if (abs(A[row][col]) > ma) {
                ma = abs(A[row][col]);
                pivot = row;
            }
        }
        // ピボットがなかったら次の列へ
        if (pivot == -1) continue;

        // まずは行を swap
        swap(A[pivot], A[rank]);

        // ピボットの値を 1 にする
        auto fac = A[rank][col];
        for (int col2 = 0; col2 < n; ++col2) A[rank][col2] /= fac;

        // ピボットのある列の値がすべて 0 になるように掃き出す
        for (int row = 0; row < m; ++row) {
            if (row != rank && abs(A[row][col]) > EPS) {
                auto fac = A[row][col];
                for (int col2 = 0; col2 < n; ++col2) {
                    A[row][col2] -= A[rank][col2] * fac;
                }
            }
        }
        ++rank;
    }
    return rank;
}

これを基本として、連立一次方程式 $Ax = b$ を解くのは以下のように実装できます。最初に $A$ と $b$ を連結させて拡大係数行列を作っています。

また、拡大係数行列を標準形にしたとき、 $A$ に対応する部分の列がすべて $0$ であるような行 $v$ に足して $b_v \neq 0$ となってはいけない (解なし) ので、それも判定しています。

template<class T> vector<T> linear_equation(Matrix<T> A, vector<T> b) {
    // extended
    int m = A.size(), n = A[0].size();
    Matrix<T> M(m, n + 1);
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) M[i][j] = A[i][j];
        M[i][n] = b[i];
    }
    int rank = GaussJordan(M, true);
    
    // check if it has no solution
    vector<T> res;
    for (int row = rank; row < m; ++row) if (abs(M[row][n]) > EPS) return res;

    // answer
    res.assign(n, 0);
    for (int i = 0; i < rank; ++i) res[i] = M[i][n];
    return res;
}

4-2. mod p の場合 (p は素数)

Gauss-Jordan の掃き出し法の実装そのものは実数の場合とほとんど同じです。掃き出し法における

行を定数倍
ある行を定数倍したものを他の行に足す

といったあたりの処理はすべて ${\rm mod}. p$ で行います。実数の場合とは異なり、数値誤差の心配がないため

ランクを求める問題
行列式を求める問題
連立方程式の解を 1 つ求める問題
連立方程式の解の個数を求める問題

などなど多彩な問題が出題される印象です。Gauss-Jordan の掃き出し法自体や連立一次方程式の解き方などは、実数の場合とほとんど同様にできます。なお、 ${\rm mod}. p$ での逆元計算が必要になりますので、このページなどを参考にしていただけたらと思います。

以下の実装では、行列の係数の ${\rm mod}. p$ の $p$ の部分をテンプレート引数に与えています。

#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;

// 逆元計算
long long modinv(long long a, long long mod) {
    long long b = mod, u = 1, v = 0;
    while (b) {
        long long t = a/b;
        a -= t*b; swap(a, b);
        u -= t*v; swap(u, v);
    }
    u %= mod;
    if (u < 0) u += mod;
    return u;
}

// matrix
template<int MOD> struct Matrix {
    vector<vector<long long> > val;
    Matrix(int n, int m, long long x = 0) : val(n, vector<long long>(m, x)) {}
    void init(int n, int m, long long x = 0) {val.assign(n, vector<long long>(m, x));}
    size_t size() const {return val.size();}
    inline vector<long long>& operator [] (int i) {return val[i];}
};

template<int MOD> int GaussJordan(Matrix<MOD> &A, bool is_extended = false) {
    int m = A.size(), n = A[0].size();
    for (int row = 0; row < m; ++row)
        for (int col = 0; col < n; ++col)
            A[row][col] = (A[row][col] % MOD + MOD) % MOD;
    
    int rank = 0;
    for (int col = 0; col < n; ++col) {
        if (is_extended && col == n-1) break;
        int pivot = -1;
        for (int row = rank; row < m; ++row) {
            if (A[row][col] != 0) {
                pivot = row;
                break;
            }
        }
        if (pivot == -1) continue;
        swap(A[pivot], A[rank]);
        auto inv = modinv(A[rank][col], MOD);
        for (int col2 = 0; col2 < n; ++col2)
            A[rank][col2] = A[rank][col2] * inv % MOD;
        for (int row = 0; row < m; ++row) {
            if (row != rank && A[row][col]) {
                auto fac = A[row][col];
                for (int col2 = 0; col2 < n; ++col2) {
                    A[row][col2] -= A[rank][col2] * fac % MOD;
                    if (A[row][col2] < 0) A[row][col2] += MOD;
                }
            }
        }
        ++rank;
    }
    return rank;
}

template<int MOD> int linear_equation(Matrix<MOD> A, vector<long long> b, vector<long long> &res) {
    int m = A.size(), n = A[0].size();
    Matrix<MOD> M(m, n + 1);
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) M[i][j] = A[i][j];
        M[i][n] = b[i];
    }
    int rank = GaussJordan(M, true);

    // check if it has no solution
    for (int row = rank; row < m; ++row) if (M[row][n]) return -1;

    // answer
    res.assign(n, 0);
    for (int i = 0; i < rank; ++i) res[i] = M[i][n];
    return rank;
}

4-3 F_2 の場合: ビットベクター高速化

いわゆる 0-1 のみを扱う世界です。

XOR 演算
ライツアウト系問題

などで自然に登場することもあり、競プロでの出題も最も多いパターンです。 ${\mathbb F}_2$ は ${\rm mod}. p$ の $p = 2$ の場合なので、基本的には ${\rm mod}. p$ と同じ実装でよいのですが、

bitset を用いたビットベクター高速化

と呼ばれるテクニックにより、定数倍高速化を行うことができます。これによって例えば $1000 × 1000$ のサイズの行列累乗や、連立方程式を解く問題にも対応できます。そのテクニックを用いた実装例を以下に挙げます:

#include <iostream>
#include <vector>
#include <bitset>
using namespace std;

const int MAX_ROW = 510; // to be set appropriately
const int MAX_COL = 510; // to be set appropriately
struct BitMatrix {
    int H, W;
    bitset<MAX_COL> val[MAX_ROW];
    BitMatrix(int m = 1, int n = 1) : H(m), W(n) {}
    inline bitset<MAX_COL>& operator [] (int i) {return val[i];}
};

int GaussJordan(BitMatrix &A, bool is_extended = false) {
    int rank = 0;
    for (int col = 0; col < A.W; ++col) {
        if (is_extended && col == A.W - 1) break;
        int pivot = -1;
        for (int row = rank; row < A.H; ++row) {
            if (A[row][col]) {
                pivot = row;
                break;
            }
        }
        if (pivot == -1) continue;
        swap(A[pivot], A[rank]);
        for (int row = 0; row < A.H; ++row) {
            if (row != rank && A[row][col]) A[row] ^= A[rank];
        }
        ++rank;
    }
    return rank;
}

int linear_equation(BitMatrix A, vector<int> b, vector<int> &res) {
    int m = A.H, n = A.W;
    BitMatrix M(m, n + 1);
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) M[i][j] = A[i][j];
        M[i][n] = b[i];
    }
    int rank = GaussJordan(M, true);

    // check if it has no solution
    for (int row = rank; row < m; ++row) if (M[row][n]) return -1;

    // answer
    res.assign(n, 0);
    for (int i = 0; i < rank; ++i) res[i] = M[i][n];
    return rank;
}