けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AOJ Course RMQ and RAQ (遅延評価セグメント木の練習問題 1)

AOJ セグメント木 【問題集】セグメント木のステップアップ データ構造テク：全体に反映させる値を別にもつ(遅延評価) 遅延評価セグメント木 【問題集】遅延評価セグメント木 StarrySkyTree データ構造 クエリ処理問題

この問題は、人生で最初に挑む遅延セグ木の問題としてオススメ！Starry Sky Tree と呼ばれるものでもある。

問題概要

数列 A_{0}, A_{1}, \dots, A_{N-1} に対して、次の 2 種類のクエリを Q 個処理せよ。なお、数列は最初は 0 に初期化されているとする。

  • クエリタイプ (0 s t x)： A_{s}, A_{s+1}, \dots, A_{t} に x を加算する
  • クエリタイプ (1 s t)： A_{s}, A_{s+1}, \dots, A_{t} の最小値を答える

制約

  • 1 \le N, Q \le 10^{5}

考えたこと

遅延セグメント木は、下図のように「区間全体の値を更新する」ことを要求されるときに効果を発揮する。

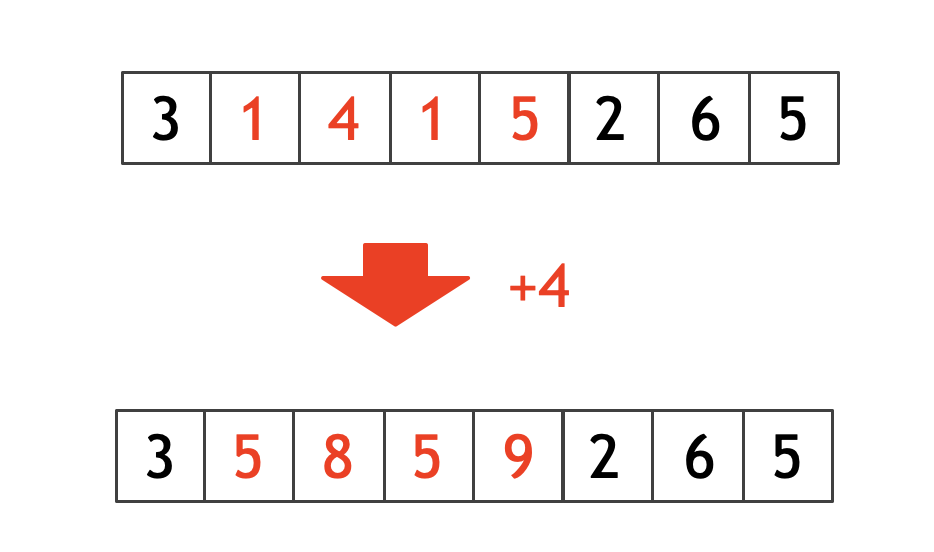
遅延セグメント木の解説は、アルメリアさんの記事がわかりやすい。

betrue12.hateblo.jp

今回のように「区間加算」「区間最小値取得」においては、

  • セグ木のノードの値：long long 型 (単位元は \infty)
  • セグ木の遅延評価パラメータの値：long long 型 (単位元は 0)

として、

  • セグ木のノード間の二項演算を表す関数：op(x, y) = min(x, y)
  • セグ木のノード値 v に遅延評価パラメータ f を適用する関数：mapping(f, v) = v + f
  • セグ木の遅延評価パラメータ f に続けてパラメータ g を合成する関数：composition(g, f) = g + f

とすればよい。

コード

#include <bits/stdc++.h>
using namespace std;


// Lazy Segment Tree
template<class Monoid, class Action> struct LazySegmentTree {
    // various function types
    using FuncOperator = function<Monoid(Monoid, Monoid)>;
    using FuncMapping = function<Monoid(Action, Monoid)>;
    using FuncComposition = function<Action(Action, Action)>;

    // core member
    int N;
    FuncOperator OP;
    FuncMapping MAPPING;
    FuncComposition COMPOSITION;
    Monoid IDENTITY_MONOID;
    Action IDENTITY_ACTION;
    
    // inner data
    int log, offset;
    vector<Monoid> dat;
    vector<Action> lazy;
    
    // constructor
    LazySegmentTree() {}
    LazySegmentTree(int n,
                    const FuncOperator op,
                    const FuncMapping mapping,
                    const FuncComposition composition,
                    const Monoid &identity_monoid,
                    const Action &identity_action) {
        init(n, op, mapping, composition, identity_monoid, identity_action);
    }
    LazySegmentTree(const vector<Monoid> &v,
                    const FuncOperator op,
                    const FuncMapping mapping,
                    const FuncComposition composition,
                    const Monoid &identity_monoid,
                    const Action &identity_action) {
        init(v, op, mapping, composition, identity_monoid, identity_action);
    }
    void init(int n,
              const FuncOperator op,
              const FuncMapping mapping,
              const FuncComposition composition,
              const Monoid &identity_monoid,
              const Action &identity_action) {
        N = n, OP = op, MAPPING = mapping, COMPOSITION = composition;
        IDENTITY_MONOID = identity_monoid, IDENTITY_ACTION = identity_action;
        log = 0, offset = 1;
        while (offset < N) ++log, offset <<= 1;
        dat.assign(offset * 2, IDENTITY_MONOID);
        lazy.assign(offset * 2, IDENTITY_ACTION);
    }
    void init(const vector<Monoid> &v,
              const FuncOperator op,
              const FuncMapping mapping,
              const FuncComposition composition,
              const Monoid &identity_monoid,
              const Action &identity_action) {
        init((int)v.size(), op, mapping, composition, identity_monoid, identity_action);
        build(v);
    }
    void build(const vector<Monoid> &v) {
        assert(N == (int)v.size());
        for (int i = 0; i < N; ++i) dat[i + offset] = v[i];
        for (int k = offset - 1; k > 0; --k) pull_dat(k);
    }
    int size() const {
        return N;
    }
    
    // basic functions for lazy segment tree
    void pull_dat(int k) {
        dat[k] = OP(dat[k * 2], dat[k * 2 + 1]);
    }
    void apply_lazy(int k, const Action &f) {
        dat[k] = MAPPING(f, dat[k]);
        if (k < offset) lazy[k] = COMPOSITION(f, lazy[k]);
    }
    void push_lazy(int k) {
        if (lazy[k] == IDENTITY_ACTION) return;
        apply_lazy(k * 2, lazy[k]);
        apply_lazy(k * 2 + 1, lazy[k]);
        lazy[k] = IDENTITY_ACTION;
    }
    void pull_dat_deep(int k) {
        for (int h = 1; h <= log; ++h) pull_dat(k >> h);
    }
    void push_lazy_deep(int k) {
        for (int h = log; h >= 1; --h) push_lazy(k >> h);
    }
    
    // setter and getter, update A[i], i is 0-indexed, O(log N)
    void set(int i, const Monoid &v) {
        assert(0 <= i && i < N);
        int k = i + offset;
        push_lazy_deep(k);
        dat[k] = v;
        pull_dat_deep(k);
    }
    Monoid get(int i) {
        assert(0 <= i && i < N);
        int k = i + offset;
        push_lazy_deep(k);
        return dat[k];
    }
    Monoid operator [] (int i) {
        return get(i);
    }
    
    // apply f for index i
    void apply(int i, const Action &f) {
        assert(0 <= i && i < N);
        int k = i + offset;
        push_lazy_deep(k);
        dat[k] = MAPPING(f, dat[k]);
        pull_dat_deep(k);
    }
    // apply f for interval [l, r)
    void apply(int l, int r, const Action &f) {
        assert(0 <= l && l <= r && r <= N);
        if (l == r) return;
        l += offset, r += offset;
        for (int h = log; h >= 1; --h) {
            if (((l >> h) << h) != l) push_lazy(l >> h);
            if (((r >> h) << h) != r) push_lazy((r - 1) >> h);
        }
        int original_l = l, original_r = r;
        for (; l < r; l >>= 1, r >>= 1) {
            if (l & 1) apply_lazy(l++, f);
            if (r & 1) apply_lazy(--r, f);
        }
        l = original_l, r = original_r;
        for (int h = 1; h <= log; ++h) {
            if (((l >> h) << h) != l) pull_dat(l >> h);
            if (((r >> h) << h) != r) pull_dat((r - 1) >> h);
        }
    }
    
    // get prod of interval [l, r)
    Monoid prod(int l, int r) {
        assert(0 <= l && l <= r && r <= N);
        if (l == r) return IDENTITY_MONOID;
        l += offset, r += offset;
        for (int h = log; h >= 1; --h) {
            if (((l >> h) << h) != l) push_lazy(l >> h);
            if (((r >> h) << h) != r) push_lazy(r >> h);
        }
        Monoid val_left = IDENTITY_MONOID, val_right = IDENTITY_MONOID;
        for (; l < r; l >>= 1, r >>= 1) {
            if (l & 1) val_left = OP(val_left, dat[l++]);
            if (r & 1) val_right = OP(dat[--r], val_right);
        }
        return OP(val_left, val_right);
    }
    Monoid all_prod() {
        return dat[1];
    }
    
    // get max r that f(get(l, r)) = True (0-indexed), O(log N)
    // f(IDENTITY) need to be True
    int max_right(const function<bool(Monoid)> f, int l = 0) {
        if (l == N) return N;
        l += offset;
        push_lazy_deep(l);
        Monoid sum = IDENTITY_MONOID;
        do {
            while (l % 2 == 0) l >>= 1;
            if (!f(OP(sum, dat[l]))) {
                while (l < offset) {
                    push_lazy(l);
                    l = l * 2;
                    if (f(OP(sum, dat[l]))) {
                        sum = OP(sum, dat[l]);
                        ++l;
                    }
                }
                return l - offset;
            }
            sum = OP(sum, dat[l]);
            ++l;
        } while ((l & -l) != l);  // stop if l = 2^e
        return N;
    }

    // get min l that f(get(l, r)) = True (0-indexed), O(log N)
    // f(IDENTITY) need to be True
    int min_left(const function<bool(Monoid)> f, int r = -1) {
        if (r == 0) return 0;
        if (r == -1) r = N;
        r += offset;
        push_lazy_deep(r - 1);
        Monoid sum = IDENTITY_MONOID;
        do {
            --r;
            while (r > 1 && (r % 2)) r >>= 1;
            if (!f(OP(dat[r], sum))) {
                while (r < offset) {
                    push_lazy(r);
                    r = r * 2 + 1;
                    if (f(OP(dat[r], sum))) {
                        sum = OP(dat[r], sum);
                        --r;
                    }
                }
                return r + 1 - offset;
            }
            sum = OP(dat[r], sum);
        } while ((r & -r) != r);
        return 0;
    }
    
    // debug stream
    friend ostream& operator << (ostream &s, LazySegmentTree seg) {
        for (int i = 0; i < (int)seg.size(); ++i) {
            s << seg[i];
            if (i != (int)seg.size() - 1) s << " ";
        }
        return s;
    }
    
    // dump
    void dump() {
        for (int i = 0; i <= log; ++i) {
            for (int j = (1 << i); j < (1 << (i + 1)); ++j) {
                cout << "{" << dat[j] << "," << lazy[j] << "} ";
            }
            cout << endl;
        }
    }
};

int main() {
    int N, Q;
    cin >> N >> Q;
    vector<long long> v(N, 0);
    const long long identity_monoid = (1LL << 31) - 1;
    const long long identity_action = 0;
    auto op = [&](long long x, long long y) { return min(x, y); };
    auto mapping = [&](long long f, long long x) { return f + x; };
    auto composition = [&](long long g, long long f) { return g + f; };
    LazySegmentTree<long long, long long> seg(v, op, mapping, composition,
                                              identity_monoid, identity_action);
    while (Q--) {
        int type, s, t;
        cin >> type >> s >> t;
        ++t;
        if (type == 0) {
            long long x;
            cin >> x;
            seg.apply(s, t, x);
        } else {
            cout << seg.prod(s, t) << endl;
        }
    }
}