問題概要

$N \times N$ のグリッドに、以下の条件を満たすように $A$ 個のルークと $B$ 個のポーンを配置することが可能かどうかを判定せよ (ルークとポーンを合わせて駒と呼ぶ)。

どのルークについても、それと同じ行・同じ列には駒ない
どのポーンについても、その上に隣接するマスには駒がない

(マルチテストケース問題)

制約

$1 \le N \le 10^{4}$
$A + B \le N^{2}$

考えたこと

まずルークは $N$ 個までしか置けない。そして、ルークを置く列は左から $A$ 列だとしても問題なく、ポーンは右側の $N-A$ 列に配置することにする。まず、明らかに $B \le (N-A)^{2}$ である。

少し具体的なケースについて手を動かして考えてみよう。たとえば $N = 7, A = 4$ のときには、下図の赤マスの位置にルークを置くことで、ポーンは黄色マスには全て置くことができる。そして明らかにこれ以上のマスには置けない。

一方、 $N = 7, A = 2$ のときには、ルークを $(7 - 2)^{2} = 25$ 個置くことはできない。ルーク自身が上下に隣接することはできないためだ。下図のような場合が最大となる。そしてよく考えると、下図のようなポーンの配置行数は、たとえ $A = 0$ であったとしても最大行数である。

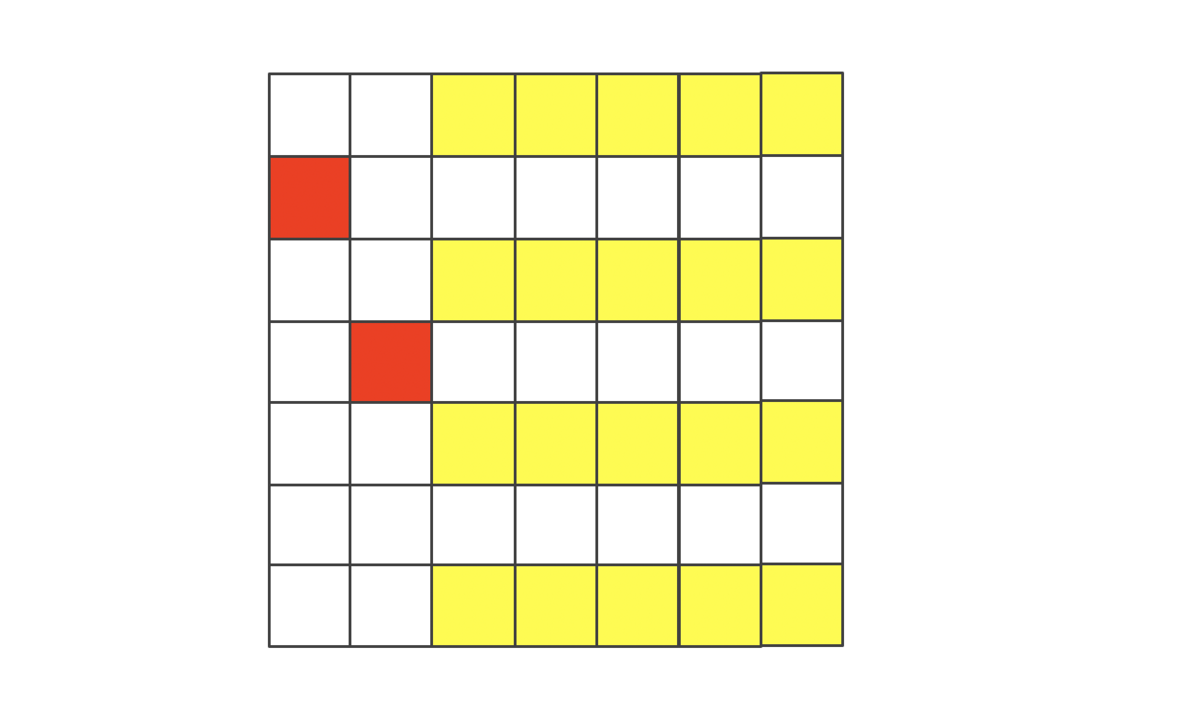
これらの場合から、ポーンの置ける個数を考えると、次の条件が浮かび上がる。

$B \le (N - A)^{2}$ でなければならない (ルークと同じ行はダメであることから)
$B \le \lfloor \frac{N+1}{2} \rfloor (N - A)$ でなければならない (ポーン同士が上限に隣接してはならないことから)

そして、

$A \le \lfloor \frac{N}{2} \rfloor$ である場合には後者がネックになる
$A \gt \lfloor \frac{N}{2} \rfloor$ である場合には前者がネックになる

ということが分かる。また、これらネックとなる最大ケースは実際に構築できることも容易にわかる。

まとめ

$A \le \lfloor \frac{N}{2} \rfloor$ のとき、 $B \le \lfloor \frac{N+1}{2} \rfloor (N - A)$ が条件
$A \gt \lfloor \frac{N}{2} \rfloor$ のとき、 $B \le (N - A)^{2}$ が条件

コード

#include <bits/stdc++.h>
using namespace std;

bool solve() {
    long long N, A, B;
    cin >> N >> A >> B;
    
    if (A > N) return false;
    else if (A <= (N / 2)) return (B <= (N + 1) / 2 * (N - A));
    else return (B <= (N - A) * (N - A));
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cout << (solve() ? "Yes" : "No") << endl;
    }
}