問題概要

.#..#..

のような長さ $N$ のマス目が与えられる。"#" は岩を表す。初期状態では、すぬけ君は $A$ マス目に、ふぬけ君は $B$ マス目にいる ( $A \lt B$ )。

今、「2 人のうちのいずれかを選んで 1 マス右か 2 マス右に移動させる」という操作を繰り返す。

この結果として、すぬけ君が $C$ マス目に、ふぬけ君が $D$ マス目にいる状態にすることは可能かどうか判定せよ。

制約

$4 \le N \le 2 \times 10^{5}$
$A \lt B$
$A \lt C$
$B \lt D$

考えたこと

いかにもエグい場合分けゲーって感じ！こどふぉではよくみるやつかもしれない。

まずとりあえず、"##" があるとそこを超えることはできないことに着目する。よって問題全体を "##" で区切ったときに、「A と C」「B と D」がそれぞれ同じ区間にいない場合は false となる。

そうでないとき、初期状態において、すぬけ君とふぬけ君が異なるグループにいる場合については自明に true となる。そうでない場合を考えると、結局次の問題に帰着される。

「与えられるマス目において "#" が連続することはないことが保証された場合」

マス目が "##" を含まない場合

改めて、今度はマス目全体を "##" ではなく "#" で区切って考えることにする。

さて、すぬけ君とふぬけ君の位置関係が入れ替わる必要があるかどうかで考えやすさが変わってくる。すぬけ君とふぬけ君とが入れ替わる必要がない場合は、最初にふぬけ君を移動させてから、すぬけ君を移動させればよいので Yes となる。

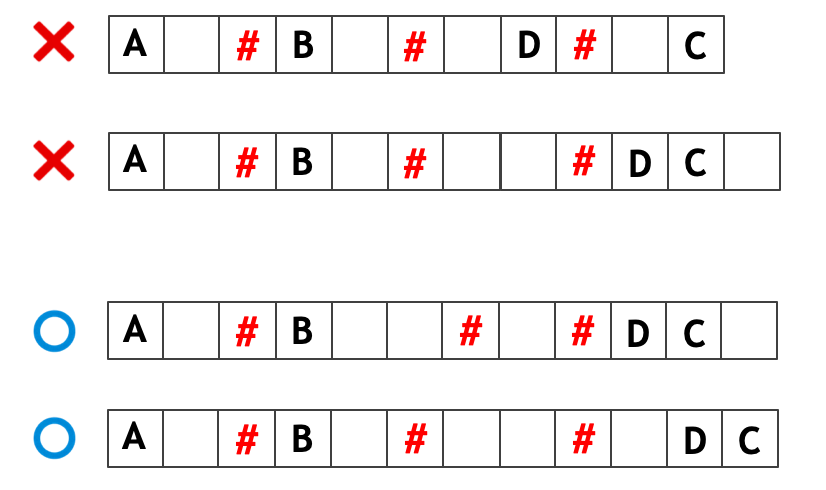
よって、すぬけ君とふぬけ君の位置関係を途中で入れ替える必要がある場合に帰着された。下図のように

B を D へと動かしていく過程でふぬけ君の両隣が通路となる瞬間が存在すれば Yes
B を D へと動かしていく過程でふぬけ君の両端が通路となる瞬間が存在しない場合は No

となる。

コード

実装上は、実際にすぬけ君とふぬけ君をスタートからゴールまで移動させられるかどうかをチェックすることにした。特にふぬけ君については、両端が空く瞬間があるかどうかもチェックすることにした。

計算量は $O(N)$ となる。

#include <bits/stdc++.h>
using namespace std;

int main() {
    int N, A, B, C, D;
    string S;
    cin >> N >> A >> B >> C >> D >> S;
    --A, --B, --C, --D;

    // マス i に移動できるか
    auto can = [&](int i) -> bool {
        if (i < 0 || i >= N) return false;
        return S[i] != '#';
    };
    // (マス i からマス j に動かせるか, 両端開く瞬間があるか)
    auto move = [&](int i, int j) -> pair<bool,bool> {
        bool open = false;
        int cur = i;
        while (cur < j) {
            if (can(cur-1) && can(cur+1)) open = true;
            if (can(cur+1)) cur += 1;
            else if (can(cur+2)) cur += 2;
            else return {false,false};
        }
        if (can(cur-1) && can(cur+1)) open = true;
        return {true,open};
    };

    // 解く
    auto solve = [&]() -> bool {
        auto snuke = move(A, C), funuke = move(B, D);
        if (!snuke.first || !funuke.first) return false;
        if (C > D && !funuke.second) return false;
        return true;
    };

    cout << (solve() ? "Yes" : "No") << endl;
}